Kompressionen
Eine Herausforderung beim Umgang mit Big data besteht darin, „den Wald vor lauter Bäumen“ nicht zu übersehen. Die Aufgabe ist es, in Terabyte von Daten die entscheidenden Informationen zu filtern.
Jetzt kann man natürlich die Frage in den Raum stellen, warum überhaupt so viele Daten erhoben werden, wenn am Ende nur ein Bruchteil davon behalten werden soll. Im Zusammenhang mit der Hochfrequenz-Analyse im Optimizer4D ist das recht einfach erklärt:
Die Abtastrate, mit der ein Signal abgetastet wird, hängt direkt mit der maximal beobachtbaren Frequenz zusammen: Aus physikalisch/mathematischen Gründen ist es nicht möglich Frequenzen zu detektieren, die höher als die Hälfte der Abtastrate liegen.
Für hohe Frequenzen, die wir beobachten wollen, benötigen wir also eine mindestens doppelt so hohe Abtastfrequenz. Um Signale bis 50Mhz beobachten zu können, müssen wir also mit mindestens 100Mhz abtasten.
Das alleine bedeutet dann schon 200MB pro Sekunde, wenn wir von 16Bit pro Wert ausgehen.
Nach der FFT Wandlung kann die Datenrate je nach Parametrierung sogar noch höher ausfallen.
Der Trick liegt darin, die Daten schrittweise zu verarbeiten, die relevante Information zu extrahieren und die Daten daraufhin zu komprimieren bzw. Zusammen zu fassen.
Dafür sind in unserer Software unterschiedliche Kompressions-Ansätze direkt in Echtzeit auf den Datenstrom anwendbar. Der Trick besteht darin, die Kompression erst nach der Frequenzwandlung anzuwenden, sodass wir unsere beobachtbare Bandbreite dadurch nicht einschränken.
Außerdem können mit unserem grafischen Programmiertool Echtzeit-Analysen mit wenigen Klicks zusammengestellt und während der Messung auf die Daten angewendet werden.
Rohsignal
Flexibilität und Anpassung
Zwischenergebnisse und weitere Datenverarbeitungsstufen können von hier beispielsweise in SQL Datenbanken gespeichert werden.
Für maximale Flexibilität können spezielle Analysen und Datentransformationen mit Hilfe von Python direkt in die Echtzeit-Analyse integriert werden.
Messungen, die auffällig erscheinen können für eine längere Vorhaltung im Roh-Format markiert werden, sodass sie später noch inspiziert werden können.
Unsere Pipeline
- Hochauflösende Digitalisierung im MHz-Bereich
- FFT-Berechnung in Echtzeit, um die volle Frequenz-Bandbreite zu beobachten
- Vor-Filterungen der FFT-Darstellung
-
- Bandfilter
- Glättungen
- Kompression
- Echtzeit-Analyse mit unserem Operatoren-Netz
-
- Erweiterung durch Python
- Speichern von Ergebnissen in Datenbank für lange Datenvorhaltung
- Markieren von auffälligen Messungen für die langfristige Speicherung
-
- Unauffällige Daten werden nach einigen Stunden verworfen
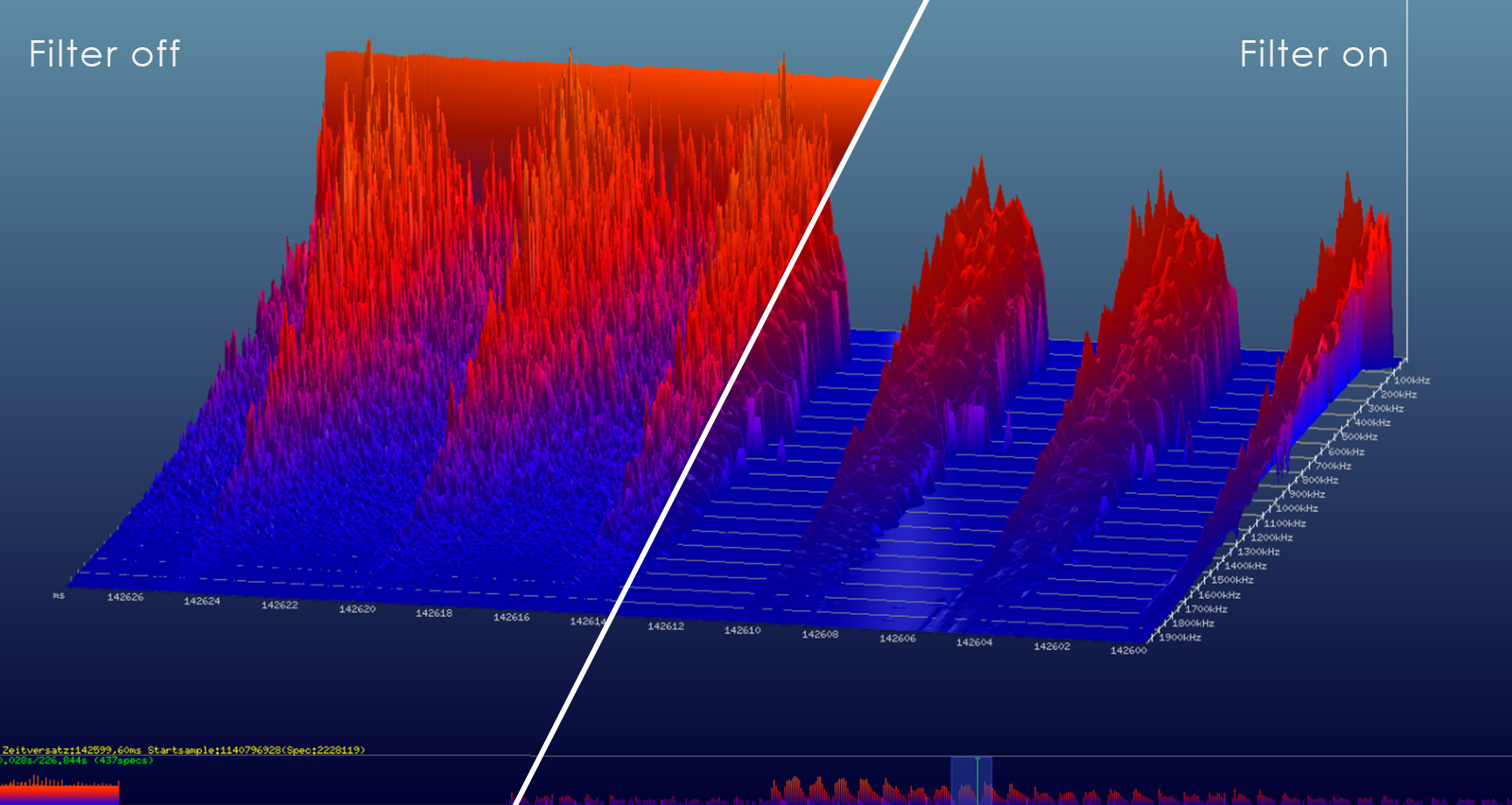
Filterung der Daten in unserer Prozesslandschaft
Kompression über Dimensionsreduktion
Dem oben beschriebenen klassischen Ansatz der Datenkompression stehen modernere Ansätze gegenüber, die die Datenkompression über eine Dimensionsreduktion realisieren. Hier stellen wir zwei Möglichkeiten in der Kurzzusammenfassung vor.
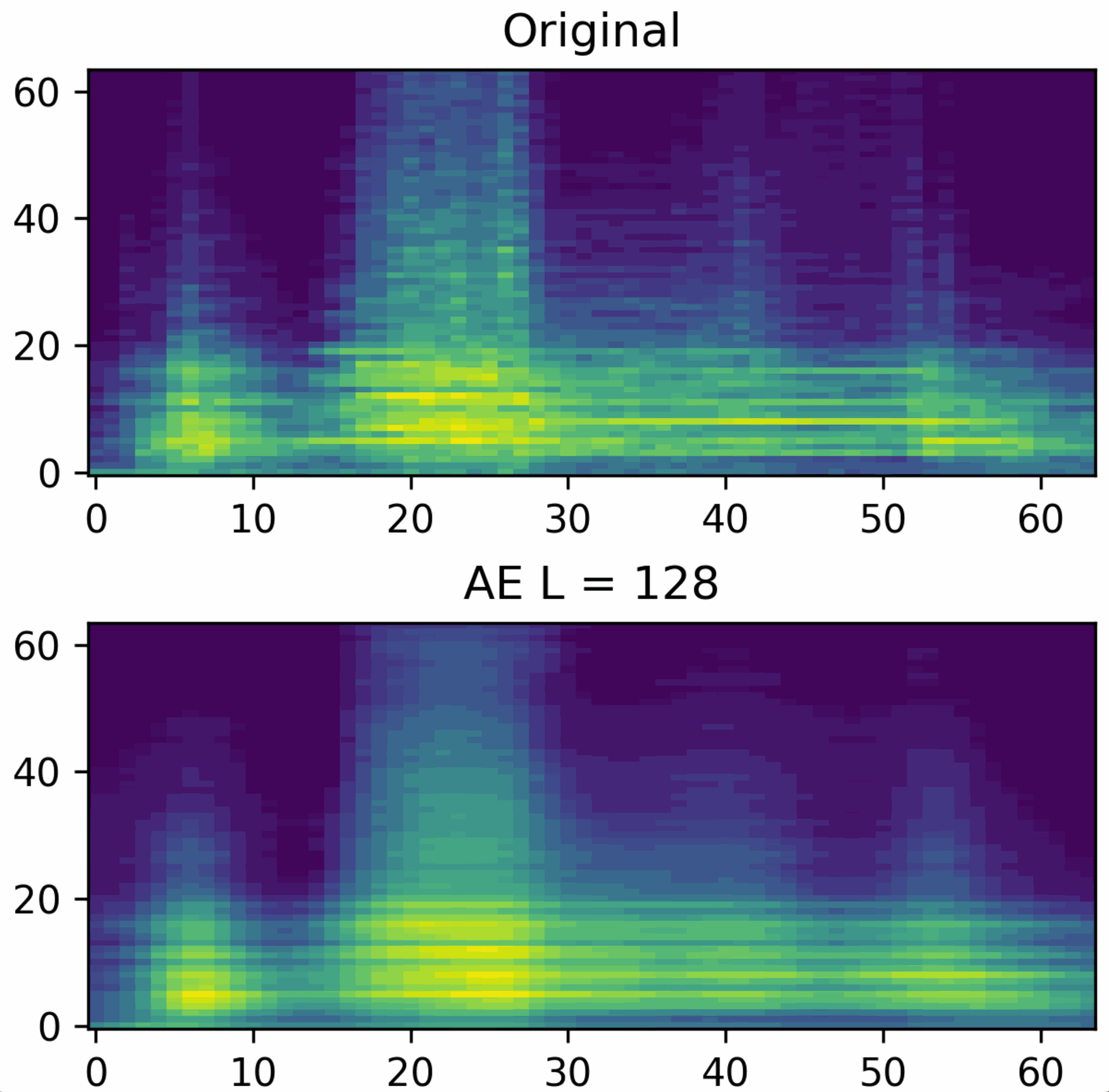
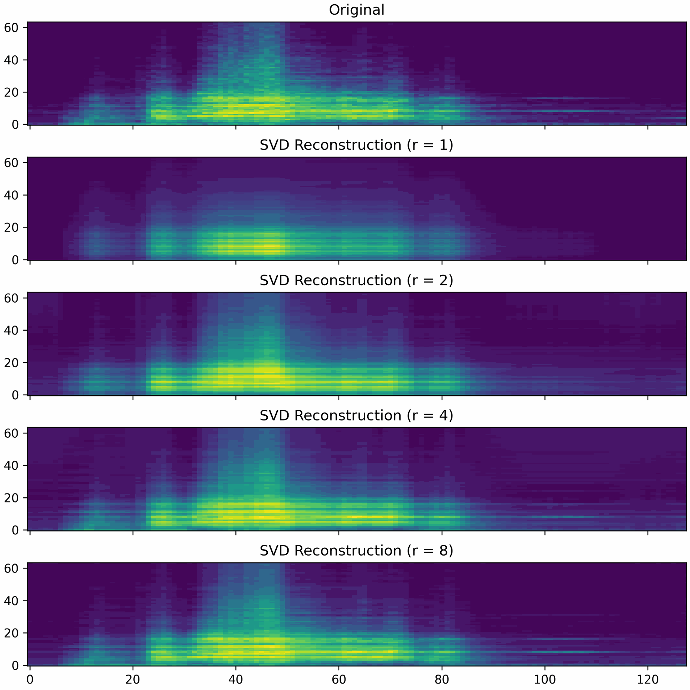
Die erste Möglichkeit der Dimensionsreduktion stellt die sogenannte Singular Value Decomposition (SVD) dar. Die SVD fasst sie Messdaten als Matrix auf und berechnet eine Zerlegung in drei Komponenten, dessen Dimensionalität wesentlich geringer ausfällt, als die der ursprünglichen Messdaten. Durch eine Multiplikation dieser drei Komponenten lassen sich die Messdaten wiederherstellen. Abhängig vom Grad der Dimensionsreduktion, auch Rang genannt, steigt die Qualität der Rekonstruktion. Ein geringer Rang hat eine starke Kompression der Daten zufolge, führt aber auch zu einem höheren Rekonstruktionfehler. Wählt man den Rang maximal, so lassen sich die Daten fehlerfrei rekonstruieren. Dafür ist der eingesparte Datenverbrauch allerdings minimal.
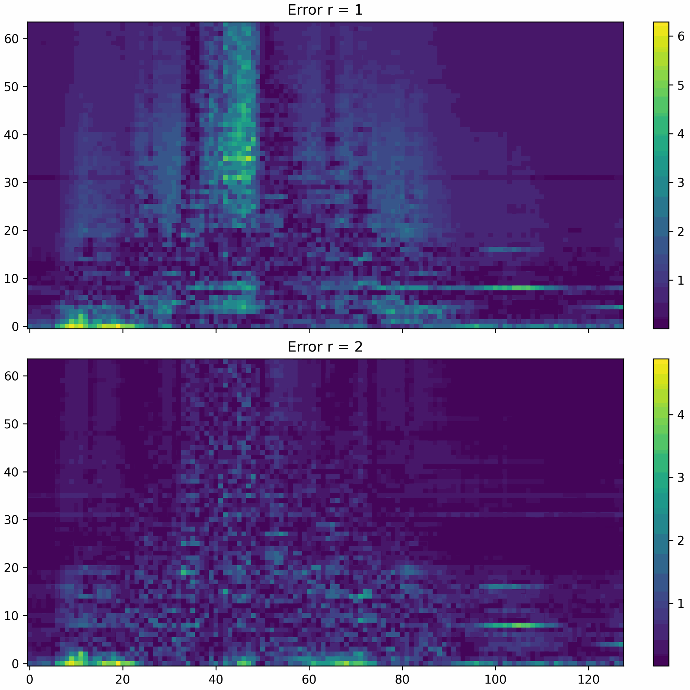
Die beiden Abbildungen unten zeigen den Fehler einer Datenrekonstruktion bei Rang 1 respektive Rang 2. Man kann erkennen, dass der Rekonstruktionsfehler Rang 1 sich stark auf bestimmte Regionen der Messdaten konzentriert, wohingegen der Fehler bei Rang 2 wesentlich geringer und gleichmäßiger verteilt ist. Wie stark die Kompression sein soll und wie gering der Rekonstruktionsfehler sein darf, hängt ganz vom Anwendungsfall ab. Entsprechend den Anforderungen muss der Rang der SVD gewählt werden.
Die Abbildungen zeigen verschiedene Rekonstruktionen mit den Rängen 1, 2, 4 und 8. Man kann deutlich erkennen, dass mit einem höheren Rang mehr Feinheiten der ursprünglichen Messdaten rekonstruiert werden.
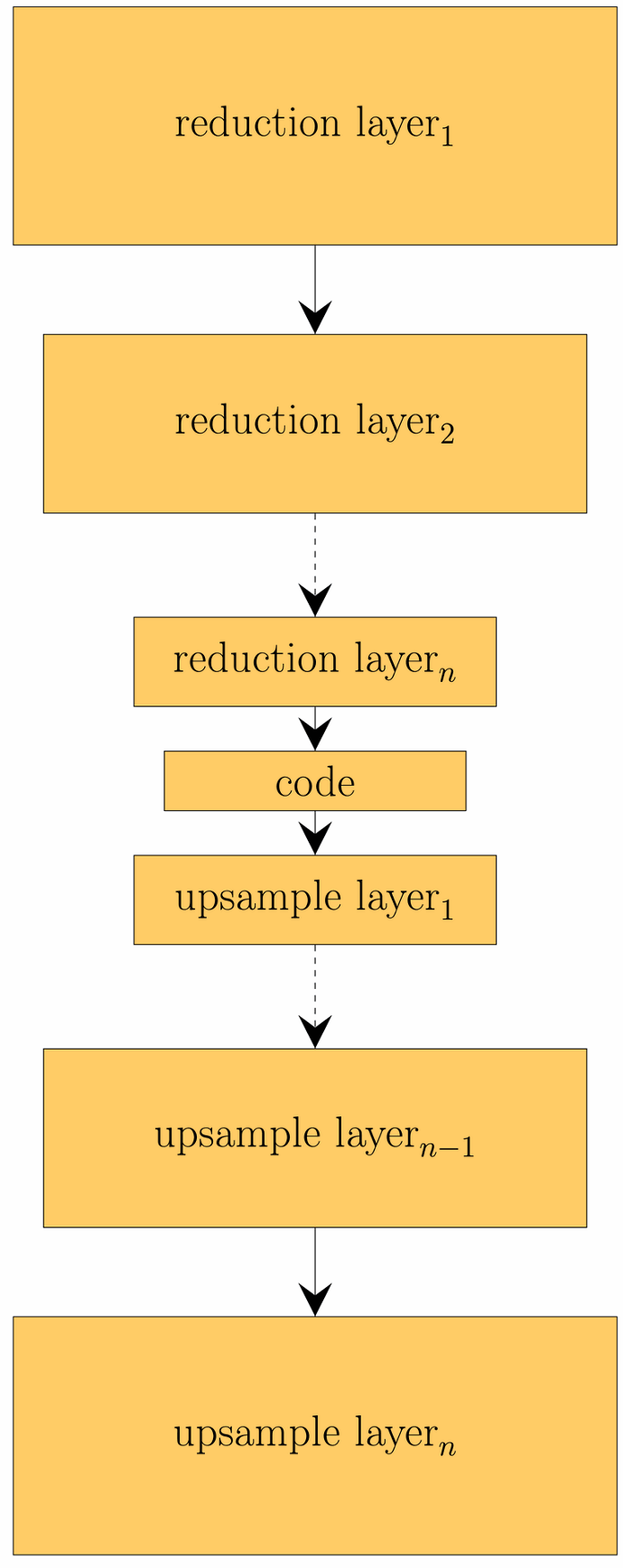
Alternativ zur SVD, kann die Dimensionsreduktion beispielsweise auch über eine Autoencoder Architektur realisiert werden. Ein Autoencoder ist eine spezielle Form von neuronalem Netz, welches aus einem Encoder und Decoder besteht.
Der Encoder reduziert die Dimensionalität der Eingangsdaten und bildet diese dabei auf einen Code ab, der die Daten repräsentiert. Über den Decoder können aus einem Code wieder die Eingangsdaten rekonstruiert werden. Diese Rekonstruktion ist in aller Regel fehlerbehaftet. Die Idee hinter dem gelernten Code ist, dass dieser komplexe Zusammenhänge der Eingabedaten repräsentiert. Dies ist ein Vorteil gegenüber SVD, die lediglich lineare Zusammenhänge darstellen kann. In der Abbildung sieht man eine Rekonstruktion mittels Autoencoder.
Die dimensionsreduzierten Repräsentationen kann nicht nur für eine Kompression genutzt werden, sondern auch für weiterführende Berechnungen.
Machine learning